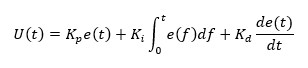D. G. Koenigsberg

D. G. Koenigsberg

Psychiatry Resident at Nuvance. Graduate of Albert Einstein College of Medicine. Researcher in deep learning applications for neuropathology at Icahn School of Medicine at Mount Sinai. Post bacc at Columbia University. Previously software engineer at Triplelift in computer vision and scalable data infrastructure. BA in Mathematics, minor in physics, from Brandeis University.

About me

Psychiatry Resident at Nuvance. MD graduate of Albert Einstein College of Medicine and a recent graduate of the Certificate in Premedical Sciences program of Columbia University. I am interested in the application of mathematics and technology to medicine and am a current researcher in the Crary Lab at Mount Sinai studying applications of machine learning in neuropathology. I have previous research experience in Combinatorics and Astrophysics. I worked as a software engineer in scalable data infrastructure at a native advertising start up called Triplelift. I also write poetry, music, and short stories.

cv/publications/talks

Bragging Rights: I…

  • Submitted a Correction to AMBOSS
  • Made this website and my wedding website
  • Own my very own canoe
  • Love my pets and travel with them
  • Collect old books1,2,3,4,5 and other old things
  • Made a ton of origami1,2,3,4,5
  • Love to bake1,2 and grow plants with my partner
  • Published my poetry in the Einstein Ad Libitum1,2 arts journal
  • Once wrote a book of lessons to teach my friend how to program in Java (who is now doing very well working as a software engineer)

Coursework Projects:

Computational Neuroscience 2018 In one of my favorite classes we were asked as a final project to create a neural encoder utilizing a spectrotemporal filter and array of Noisy Leaky IAF "trigger and fire" neurons. The leaky IAF is an encoder of a signal into a train of spikes that is meant to approximate the traditional Hodgkin and Huxley neuron quite well by preserving the nonlinear nature of the Hodgkin and Huxley neuron without the sacrifice of needless computation time. In this way neurons translate amplitude signals into a frequency based sampling space.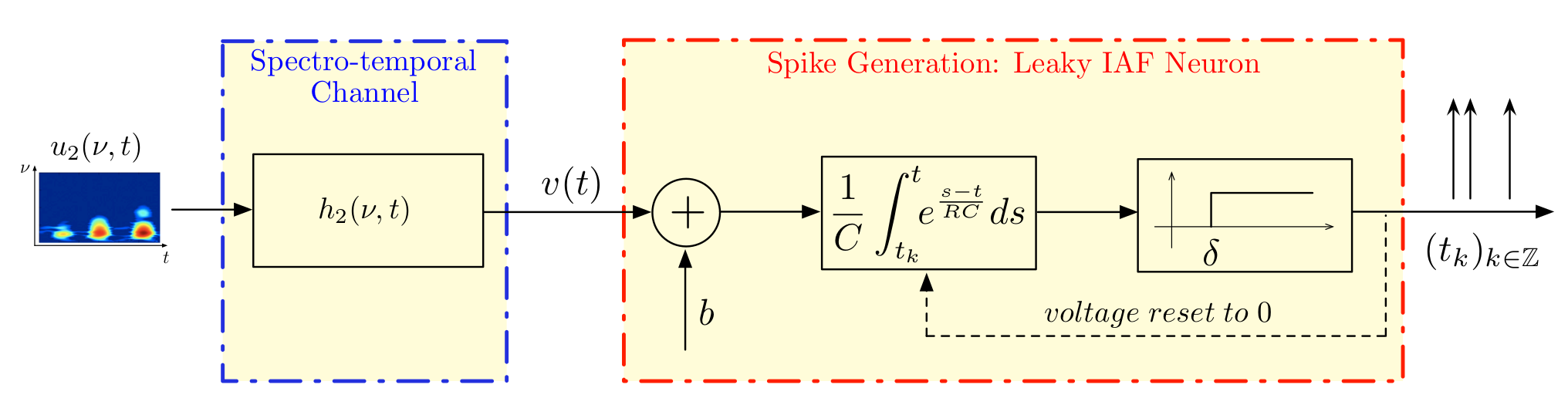

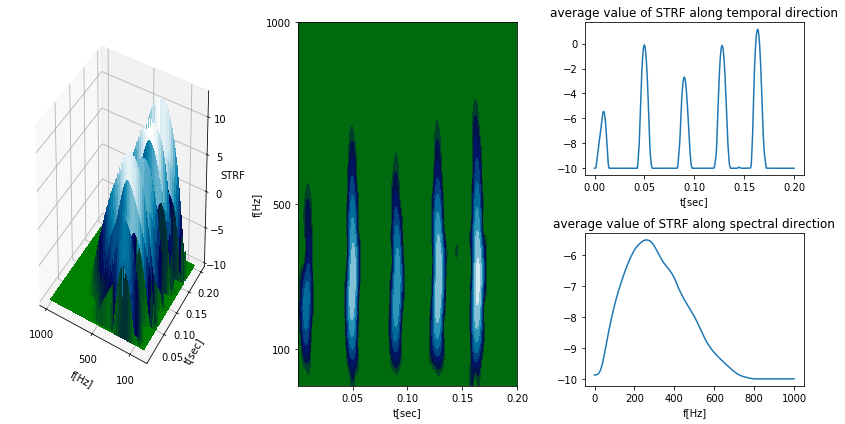
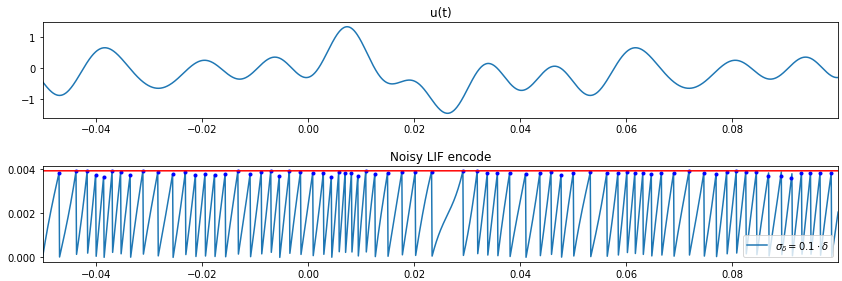
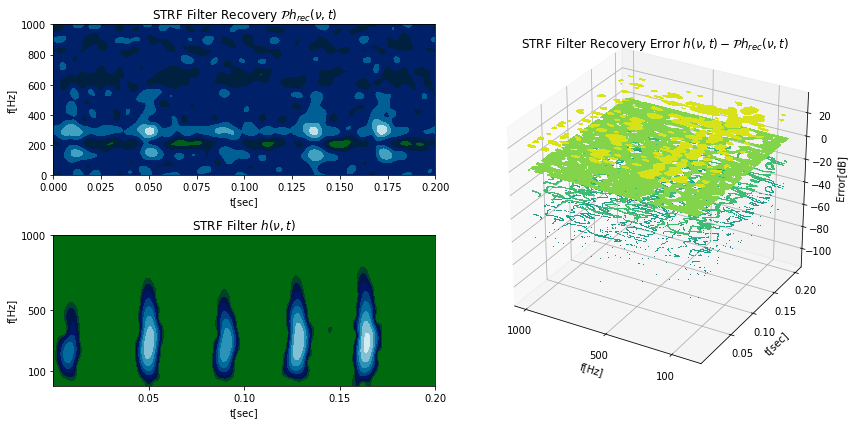
Above is a schema of the proposed project. A signal is passed in the two dimensional space of frequency and time into the spectrotemporal filter. The resulting signal is added to a bias and fed through the leaky IAF. The claim is that using the right analysis (handwaving aside) we can mathematically recompute the filter from the spike train. This same method of inquiry could in theory be applied to real neurons in order to determine the filtering occurring at the axon hillock.

Above is a diagram of the initial spectrotemporal filter. Different two dimensional and three dimensional views are provided.

Above is the resulting spike train of passing the signal (on top) through the circuit and adding noise proportional to the firing threshold.

Once we have the spike times, we are able to recover an approximation of the spectrotemporal filter. Some discrepancies exist where the filter value changes suddenly (i.e. where it approaches its minimum of -10). This is because in the filter is effectively zeroes and its bandwidth is effectively infinite. This method is limited computationally wherever the bandwidth is sufficiently high, however the approximation of the filter is still quite good. This approach can be used to describe neurological phenotypes in various disease states (as is the case here).
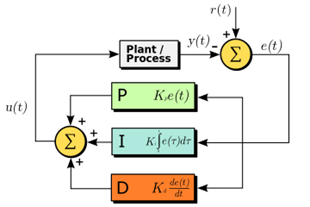
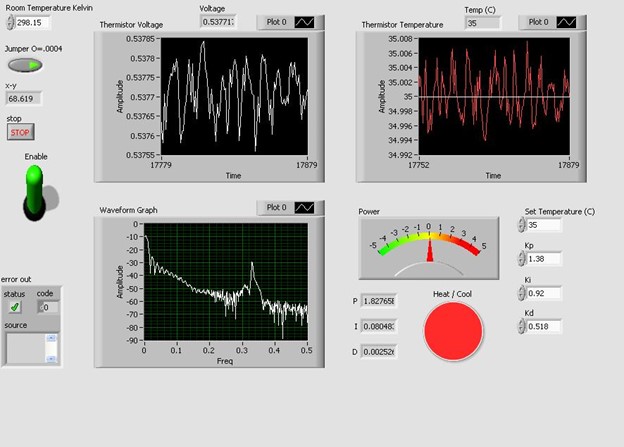
Advanced Physics Lab 2013 In one of my favorite experiments way back in college we were tasked with building a PID controller. The idea behind the PID controller is that you have a real value you want your program to accomplish but you only have access to some kind of power which moves you in the direction of that real world value. In the real world things like momentum, resistance, and error complicate problems and simply setting your power proportional to the difference between your desired real world value and the current one doesn't work optimally. Take for instance an air conditioning unit. The AC unit only knows different power settings, what the current temperature is, and what the desired temperature is. If it rapidly cools down a room to a desired temperature it may overshoot. The process of optimally approaching a given value is far more important when applied to autopilot systems or robots used in surgery.

In a PID controller the difference between your desired value and your current value is referred to as the error (this can be confusing because there is probably error between your current value and your measured current value). We set our power proportionally to the error, the integral of the error over time, and the derivative of the error over time (all approximated numerically).

This gives us an equation with a bunch of mysterious constants. The job of optimally determining the best values has been done for us by Ziegler and Nichols. We must simply find the value for which the proportional portion of our PID creates a simple wave. This can be done by fine tuning and inspection, or robustly it can be done by taking the fast Fourier transform of the data and finding the frequency with the highest peak.

The experiment was conducted and programmed in labVIEW where a given temperature was set for a thermoelectric generator.

In the above there is a tight approximation of 35 degrees Celsius by the PID controller (top right). The fast Fourier transform is also displayed showing a peak of about 3.2 Hz (bottom left). This enabled us to optimally set the coefficients (right side) and build a very reactive PID controller.

MOTIVATE Lab: